Hi Luis,

I drew a circle, divided into quarters and labeled three points.

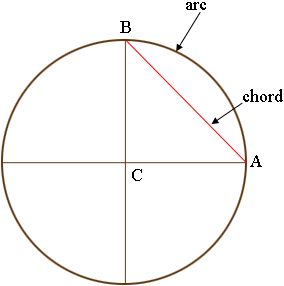
The straight line joining $A$ and $B$ is called a chord and the curved part of the circle joining $A$ and $B$ is called an arc. I'm not sure which length you want.

The circumference of a circle, the distance all the way around, is $\pi$ times the diameter where $\pi$ is approximately 3.1416. The arc from $A$ to $B$ is one quarter the way around and hence, if the diameter is 100 feet then the length of the arc is

\[\frac14 \times \pi \times 100 = 78.54 \mbox{ feet.}\]

The triangle $ABC$ is a right triangle and for a right triangle Pythagoras Theorem says that the square of the hypotenuse, the side opposite the right angle, is the sum of the squares of the lengths of the other two sides. Thus if the diameter of the circle is 100 feet then the two sides $BC$ and $CA$ are each of length 50 feet and hence

\[|AB|^2 = 50^2 + 50^2 .\]

Thus the length of the chord $AB$ is

\[|AB| = \sqrt{50^2 + 50^2} = \sqrt{2500 + 2500} = \sqrt{5000} = 70.71 \mbox{ feet.}\]

Write back if I have misinterpreted your question or if we can be of any further help.

Harley