Hi Marcus,

I drew a diagram of the funnel at a time $t$ seconds. My funnel has radius $R$ inches and height $H$ inches. At the time $t$ seconds the radius of the top of the water is $r = r(t)$ inches, the height of the water is $h = h(t)$ inches and the volume $V = V(t)$ in cubic inches is given by

\[ V(t) = \frac13 \pi\; r^2(t) h(t)\]

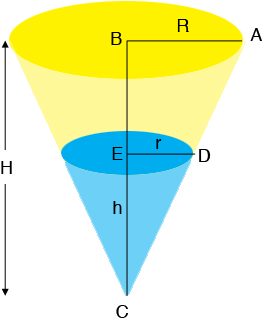
You also know for this problem that $\frac{dV}{dt} = -1$ cubic inches per second and that you want to find $\frac{dh}{dt}$ at a particular time.

The challenge now is to find a relationship between $r(t)$ and $h(t)$ so that you can write the expression for $V(t)$ above in terms of $h(t)$ alone. The fact that I am going to use is that triangles $ABC$ and $DEC$ are similar and hence $\frac{R}{H} = \frac{r}{h}.$ Substitute the values you have for $R$ and $H,$ solve for $r$ and substitute into the equation for $V(t)$ and differentiate both sides of the resulting expression with respect to $t.$ Evaluate this at the time when the water level is 2 inches from the top.

If you have trouble completing this problem write back, tell us what you have done and we will try to help.

Penny