Hi Melanie,

Here is a sketch of a random variable $X$ which has the normal distribution with mean mu, $(\mu)$ and standard deviation sigma $(\sigma).$

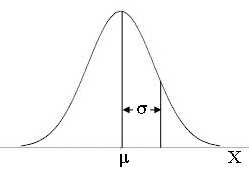
The area bounded by the curve and the X-axis is 1 and the curve is symmetric about $X = \mu$ and hence the area under the curve to the left of $X = \mu$ must be 1/2. This area is the probability that $X$ is less than $\mu$ and hence

\[Pr(X < \mu) = \frac12 .\]

In your example $mu = 40,000$ miles and you would expect half of the tires in the sample to last less than 40,000 miles. Thus the answer to part c) is 5,000 tires.

To answer the remaining parts of this problem you need to convert $X$ to the standard normal distribution and use a standard normal distribution table. I'll do part b) for you and you can do the rest. Here is the diagram I drew.

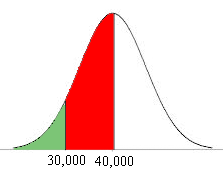
Normal distribution with $\mu = 40,000$ and $\sigma = 5,000.$

The probability that $X$ is between 30,000 and 40,000 miles is the area under the curve between 30,000 and 40,000, the red area in the diagram. To calculate this probability I am going the calculate the area under the curve to the left of 30,000 miles, that area shaded green in the diagram and then

\[Pr(30,000 < X < 40,000) = Pr(X < 40,000) - Pr(X < 30,000).\]

Since I already know that $Pr(X < 40,000) = \large \frac{1}{2}$ I only need to find $Pr(X < 30,000).$ To do this I need to use the standard normal distribution.

To convert a normal random variable with mean mu and standard distribution to the standard normal random variable $Z$ the conversion is

\[Z = \frac{X - \mu}{\sigma}\]

which in your case is

\[Z = \frac{X - 40,000}{5,000}.\]

Hence

\[Pr(X < 30,000) = Pr \left( \frac{X - \mu}{\sigma} < \frac{30,000 - 40,000}{5,000} \right) \]

or

\[Pr(X < 30,000) = Pr\left( Z < -2 \right).\]

Again by the symmetry of the normal distribution $Pr(Z < -2) = Pr(Z > 2).$ (If this isn't clear look at a diagram.)

My standard normal table gives probabilities of the form $Pr(0 < Z < a)$ for various values of $a$ and in particular it gives $Pr(0 < Z < 2) = 0.4772$ and hence $Pr(Z > 2) = \frac12 - Pr(0 < Z < 2) = 0.0223.$

Finally

\[Pr(30,000 < X < 40,000) = Pr(X < 40,000) - Pr(X < 30,000) = \frac12 - 0.0223 = 0.4772.\]

and thus the number of tires expected to last between 30,000 and 40,000 miles is

\[10,000 \times 0.4772 = 4,772.\]

Penny