Hi Mike,

I drew a diagram of your frustum and expanded to to show the entire cone and included some labels.

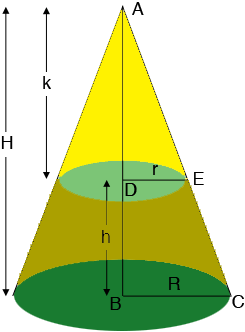
From the diagram the volume of the frustum is the volume of the cone with base $R$ and height $H$ and the cone with base $r$ and height $k.$ The volume $V$ of a cone is given by

\[V = \frac13 \pi \; \left(\mbox{ base radius}\right)^2 \times \mbox{ height.}\]

You know the radius of each of the cones so to complete the calculation you need the values of $A$ and $a.$ One additional fact you know is that

\[H = h + k.\]

The mathematical fact that allows you to complete the calculation is that triangles $ABC$ and $ADE$ are similar and hence

\[\frac{|AB|}{|BC|} = \frac{|AD|}{|DE|}\]

or

\[\frac{H}{R} = \frac{k}{r}.\]

Substitute $H = h + k$ in the equation above and solve for $k.$ Since $H = h + k$ you now have all the information you need to complete the calculation of the volume of the frustum.

Penny