Cutting a hexagon from a disk

HOME

Math Central

Quandaries & Queries

Question from Paul:

I am a machinist and sometimes need to make a hex from round material.
If I know the distance of the flat sides opposite one another of my hex, how can I calculate the size of material I need to turn to give me the right diameter to finish the part with six sides?

Hi Paul,

I am going to let $d$ be the diameter of the disk you need to turn and $w$ the width of the hexagon, the distance between the flat sides. Thus in my diagram the distance from $C$ to $B$ is $\large \frac{d}{2}$ and the distance from $C$ to $D$ is $\large \frac{w}{2}.$

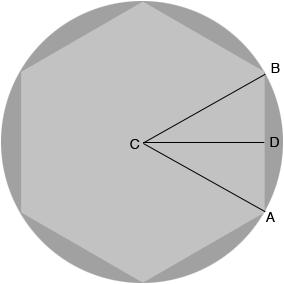
hexagon in a disk

The measure of the angle $BCA$ is $\large \frac{360}{6} \normalsize = 60$ degrees and hence the measure of the angle $BCD$ is 30 degrees. Hence

\[ \cos (30) = \frac{\sqrt{3}}{2} = \frac{|CD|}{|CB|} = \frac{w/2}{d/2}\]

and thus

\[d = \frac{2}{\sqrt{3}} w = 1.1547\; w.\]

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.