| |||
| Math Central | Quandaries & Queries |
|
Question from Rahul, a student: find the area of the quadrilateral whose side measure9cm,40cm,28cm,15cm and in which the angle between the first 2 sides is a right angle |
Rahul,
I drew a diagram (not to scale) of what you described. $|AB| = 9, |BC| = 40, |CD| = 28$ and $|DA| = 15$ centimeters.
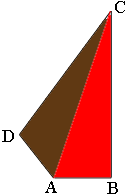
I joined $A$ to $C$ to partition the quadrilateral into 2 triangles. Triangle $ABC$ is a right triangle and its area is easy to calculate. Also since triangle;e $ABC$ is a right triangle you can use Pythagoras Theorem to find the length of the line segment $CA.$
You are left with triangle $CDA$ and you know the lengths of all three of its sides. To find its area look at the second paragraph in my response to Saba.
Penny
 |
||
Math Central is supported by the University of Regina and the Imperial Oil Foundation.