Hi Rayven,

For your first function I would begin by plotting $g(x) = x + 3.$ Hopefully you know by the form of the function the graph is a line so you need only plot two points and the draw he line that passes through them. You can choose any two points, I chose $x = 0$ which gave $f(x) = f(0) = 3$ and $x = 2$ which gave $f(x) = f(2) = 5.$ I then plotted these two points in turquoise and drew the graph of $g(v).$

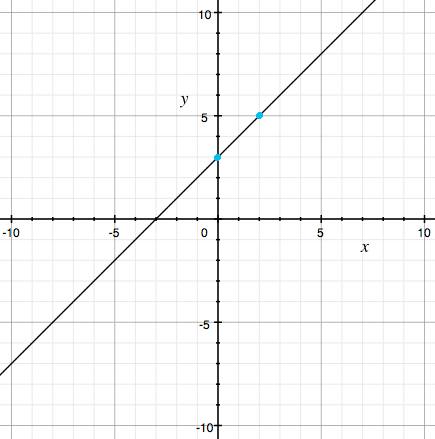
y = g(x) = x + 3

How does this graph change if the function is

\[f(x)= |x+3 | \mbox{ for }-5 ≤x≤ 3?\]

First of all $f(x)$ is defined for $-5 \leq x \leq 3$ so you need to erase the part of the graph with $x < -5$ and the part of the graph with $x > 3.$

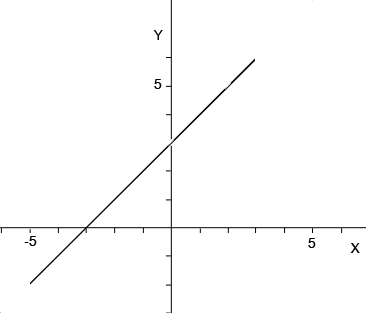
\[g(x)= x+3 \mbox{ for }-5 ≤x≤ 3?\]

What effect does the absolute value have on the graph? If a point $(x, g(x)),$ on the graph of $g(x)$ is on or above the X-axis then $x + 3 \geq 0$ so $f(x) = g(x)$ and the point is on the graph of $f(x).$ If a point $(x, g(x)),$ on the graph of $g(x)$ is a certain distance below the X-axis then $f(x) = -g(x)$ so the point $(x, f(x))$ is the same distance above the X-axis. Thus the piece of the graph of $g(x)$ below the X-axis is reflected in the X-axis to appear above the X-axis.

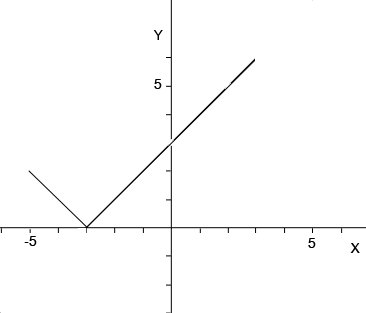
\[f(x)= |x+3 | \mbox{ for }-5 ≤x≤ 3?\]

For your second problem I think you have one of the inequalities pointing the wrong way so I am going to change the function to

f(x)= {x if x ≤ 0
        {x+1 if x > 0

would start by plotting $y = x$ and $y = x + 1$ on the same graph. You only want the piece of $y = x$ for $x \leq 0$ so erase the part of $y = x$ which has $x > 0.$ Likewise you only want the part of $y = x + 1$ with $x > 0$ so erase the part of $y = x + 1$ that has $x \leq 0.$

Penny