| |||
| Math Central | Quandaries & Queries |
|
Question from steve, a student: using 6" wide boards how many inches would each of 4 boards equal in length need to be to produce a square with an inside perimeter of 84 inches on a side? what is the exterior perimeter? There is to be 45 degree cuts at each end of each board. |
Hi Steve,
I drew a diagram of what I think you are describing.
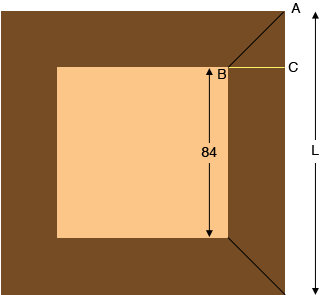
Since the angle $ABC$ measures $45^o$ triangle $ABC$ is an isosceles triangle and the lengths $|BC|$ and $|CA|$ are equal. Hence the length $L$ is $84 + 2 \times |BC| \mbox{ inches }$ that is 84 inches plus twice the width of the board.
Harley
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.