Hi Steve,

I drew what you described with L1 along the X-axis and L2 along the Y-axis. Thus in my diagram a = 10' 5", B = 10' 6" and c = 3' 3".

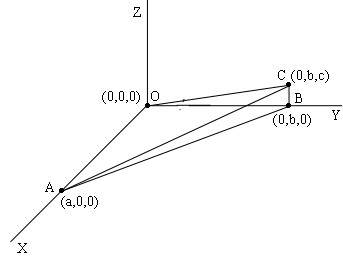
There is a theorem in mathematics that says take if you have a region R in the plane with an area and a point P not in the plane and you form a "pyramid" by joining every point in R to P then the volume of the pyramid is $\frac13 \times \mbox{ the area of the base} \times \mbox{ the height of P above the plane.}$ This is the situation you have. R is the triangle OAB and P is the point C. Thus the volume of your wedge is

\[\frac13 \times \left( \frac12 \times a \times b \right) \times c = \frac{a b c}{6}\]

I suggest that you change all the dimensions to inches, find the volume in cubic inches and then divide by $12 \times 12 \times 12 = 1728$ to obtain the volume in cubic feet.

Penny