Hi Tim,

In a response to a similar question I gave the layout for a cone if you know the radius of the base $R$ and the height $H.$ You have $R = 15$ inches but you don't have the height. In my diagram of your cone below $|CA| = 15$ inches and the measure of angle $CAB$ is $30^o.$

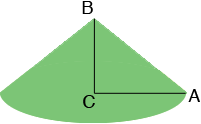
Since angle $BCA$ is a right angle the measure of angle$ABC$ is $60^o$ and triangle $ABC$ is a 30-60-90 triangle. The lengths of the sides of a 30-60-90 triangle ate $1:2:\sqrt3$ where 2 is the length of the hypotenuse. Thus in triangle $ABC$ the length of the side $BC$ is $\frac{15}{\sqrt3}.$ Thus $H = \frac{15}{\sqrt3}$ and you can apply the expressions in my response noted above.

Write back if you need more assistance,
Penny