| |||
| Math Central | Quandaries & Queries |
|
Question from Veronica, a student: A man flies a kite at a height of 120 meters. The wind carries the kite horizontally away from him at a rate of 8 meters/second. How fast is the distance between the man and the kite changing when the kite is 130 meters away from him? |
Hi Veronica,
In my diagram the man is at $M,$ the kite is at $K$ and$ $O is 120 m directly overhead of $M.$
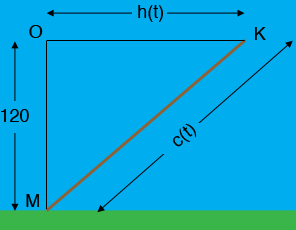
The horizontal distance from O to K is $h(t) \mbox{ meters }$ and the length of the cord holding the kite is $c(t),$ both at time $t$ seconds. You know that $h^\prime(t) = 8$ meters/second.
Use Pythagoras Theorem to find an expression for $c(t).$ Differentiate both sides of this expression with respect to $t$ and evaluate at the time when $h(t) = 130 \mbox{ meters. }$ Use your expression for $c(t)$ to find its value at this time.
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.