| |||
| Math Central | Quandaries & Queries |
|
Question from Veronica, a student: A container is the shape of an inverted right circular cone has a radius of 1.00 inches at the top and a height of 5.00 inches. At the instant when the water in the container is 1.00 inches deep, the surface level is falling at the rate of -2.00 inches/second. Find the rate at which the water is being drained. |
Hi Veronica,
Here is my diagram of the container at a time $t$ seconds.
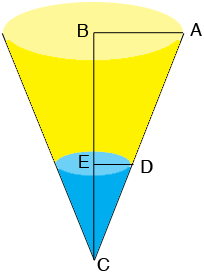
The length of $AB$ is 1 inch and the length of $BC$ is 5 inches. Let $h(t)$ be the length of $EC$ and $r(t)$ be the length of $DE,$ both in inches. These are both functions of time.
The volume of a cone is
\[V = \frac13 \pi \; r^2 h.\]
Use the fact that triangles $ABC$ and $DEC$ are similar to find a relationship between $r(t)$ and $h(t)$ and then use this relationship to eliminate $r$ from the expression for the volume $V$ of the cone $DEC.$
The volume of the cone $DEC$ is a function of time and hence you can differentiate both sides of the new expression for the volume to obtain an equation with $V^\prime (t)$ on the left and an expression involving $h(t)$ and $h^\prime (t)$ on the right. Use the values of $h(t)$ and $h^\prime (t)$ when $h(t) = 1$ inch to find the value of $V^\prime (t)$ at this time.
Penny
 |
||
Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.