The area of an irregular octagon

HOME

Math Central

Quandaries & Queries

Question from zafar, a student:

if i have a rectangular octagon then how i can find its area
1. The length of rectangle is 42 and the width is 21 and and the base length is 42-12 =30 i mean the
length of base =30

Hi Zafar,

Is this the octagon you had in mind?

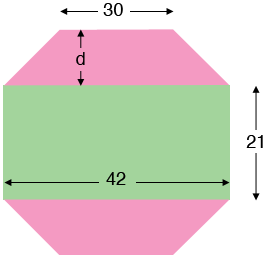
octagin

If so then the octagon can be partitioned into there pieces, a rectangle, which is 42 units by 21 units and hence has an area of $42 \times 21$ square units, and two congruent trapezoids. The area of a trapezoid is the average of the lengths of the parallel sides times the distance between the parallel sides. Thus in my diagram each of the pink trapezoids has area $\large \frac{42 + 30}{2} \normalsize \times d$ square units. Thus to complete the area calculation you need to know the distance $d.$

Penny

Math Central is supported by the University of Regina and The Pacific Institute for the Mathematical Sciences.