Hi Zuhdina,

Unfortunately there is no nice, neat algebraic solution to this problem. You mentioned logarithms and you can take the logarithm of each side to get

\[x \log(2) + 3log(5) = 4 \log(x)\]

which s no simpler than the equation you had to start. The best you can do is to approximate a solution.

My first step would e to define $f(x)$ by

\[f(x) = 2^x \times 5^3 - x^4\]

and use computer software or a graphing calculator to plot $y = f(x)$ and see where the graph crosses the x-axis. The graphing software on my computer gave me

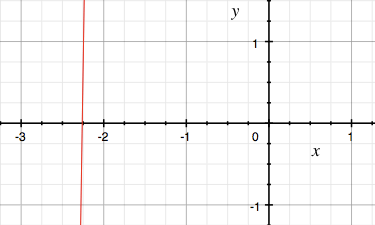
The curve is in red so from the graph I can see that $f(x) = 0$ when x is approximately -2.25.

To obtain a better approximation I would use Wolfram Alpha. I typed in solve 2^x * 5^3 - x^4 = 0 and obtained $x = -2.26014.$

Penny