Hi Ana,

Without the diagram this is difficult. I can guess what the diagram looks like but I think there is a piece of information missing.

Penny

Ana wrote back.

With the diagram may you help me please?

You still didn't send a diagram so the best I can do is guess. I think the diagram looks something like this.

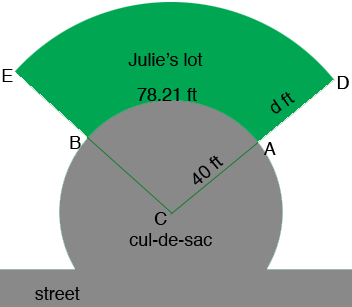
I want to find the area of the sector $ABC$ and to do so I am going to use the symmetry of the circle. The area of the sector $ABC$ is a fraction of the area of the circle of radius 40 ft. The length of the arc $AB$ is a fraction of the circumference of the circle of radius 40 ft. By the symmetry of the circle these two fractions are the same. Thus

\[\frac{\mbox{area of the arc ABC}}{\pi \; 40^2} = \frac{78.21}{2 \pi \; 40}\]

and hence

\[\mbox{area of the arc ABC} = \frac{78.21}{2 \pi \; 40} \times \pi \; 40^2 = 156.24 \mbox{ square feet.}\]

Do you know the depth of Julie's lot, the distance $d$ in my diagram? If so you can use the procedure I used above to find the area of the sector $DEC,$ and then the area of Julie's lot is the difference in the areas of the two sectors.

I hope this helps,

Penny