Hi Arun,

Suppose you have a circular cylinder of diameter $d$ mm and height $h$ mm and you slice it from the bottom right to the top left as in the diagram. By the symmetry of the circle, the surface area of the piece removed (the green piece) is equal to the surface area of the piece you keep (the pink piece). Hence the surface area of the piece you keep is half the surface area of the cylinder.

To find the surface area of the cylinder slice it along one of the vertical lines and roll it out flat. What you get is a rectangle of height $h$ mm and length, the circumference of the base circle which is $\pi \; d$ mm and hence the surface area of the piece you keep is $\frac12 \pi \; d \times h$ square mm.

For your question you know $d = 630 \mbox{ mm}$ so all that remains is to find $h.$ For this we can use some trigonometry.

A vertical cross-section of the cut pipe shows a right triangle $ABC$ with $CA$ the diameter of the pipe, $BC$ the height of the cylinder and angle $CAB$ the angle of the cut which in your case is $22.5^{o}.$

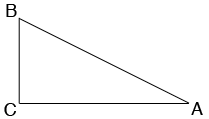
The tangent of the angle $CAB$ is the length of $BC$ divided by the length of $CA$ and hence

\[\tan 22.5^o = \frac{h}{d}\]

or

\[h = d \times \tan 22.5^o = 630 \times 0.4142 = 260.95 \mbox{ mm.}\]

Thus the surface area of the pink piece in my diagram is

\[\frac12 \pi \; d \times h = \frac12 \pi \; \times 630 \times 260.95 = 258,241 mm^{2}.\]

Harley