| |||
| Math Central | Quandaries & Queries |
|
Question from Brayden, a student: Show that a tangent line drawn to the curve y=x^3 at the point (d,f (d)), where d>0, forms a right triangle with the x and y axes in quadrant 4 whose area is (2/3)d^4. |
Hi Brayden,
I find it really helps to draw a sketch. In my sketch of the curve $y = x^3$ $O$ is the origin, $T$ is the point of tangency, $P$ and $Q$ are the points where the tangent intersects the $X$ and $Y$ axes and the $X$ coordinate of $T$ is $d.$
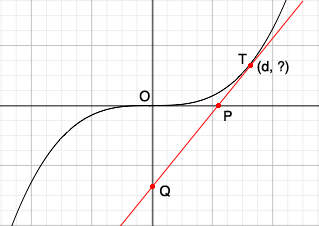
$T$ is on the curve $y = x^3$ and its first coordinate is $d.$ What is its second coordinate? What is the slope of the tangent to $y = x^3$ at $T?$ Write the equation of the tangent line and find the coordinates of $P$ and $Q.$ What is the area of the triangle $POQ?$
Penny
 |
||
Math Central is supported by the University of Regina and the Imperial Oil Foundation.