| |||
| Math Central | Quandaries & Queries |
|
Question from Casey: I have an equilateral triangle inscribed in a circle - this triangle has been bisected to give me 2 right triangles. I know the length of the line bisecting the equilateral triangle is 36 inches. How do I figure out the circumference of the circle and the length of the sides of the equilateral triangle? |
Hi Casey,
The key to this problem is that in any triangle with angles that measure 30, 60 and 90 degrees the lengths of the sides are in the ratio of $1: 2: \sqrt{3}.$
I drew a diagram of with the center of the circle at $C$ and added a line segment from $C$ to $A,$ one of the vertices of the triangle.
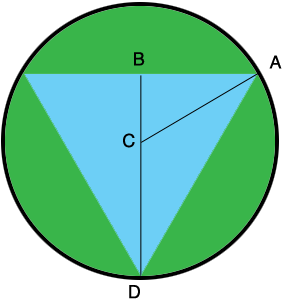
Can you complete the problem now?
Write back if you need more assistance,
Penny
 |
||
Math Central is supported by the University of Regina and the Imperial Oil Foundation.