Hi Chirag,

Suppose you have a round bar that has a radius of $r$ units and a height of $h$ units, then the surface is composed of three pieces, two circular disks of radius $r$ units and the curved piece that forms the side.

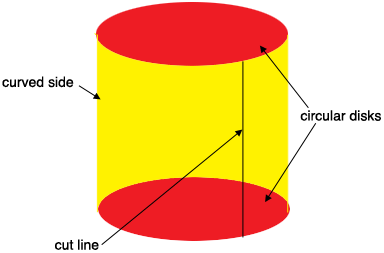
Imagine that the diagram represents the surface only, like an empty soup can. Cut off the top and bottom to obtain two circular discs of radius $r$ units. The area of a circular disk is

\[\pi \; r^2 \mbox{ square units.}\]

Now cut along the cut line in the diagram and roll the curved side out flat. Yo have a rectangle of height $h$ unit and length the circumference of the circular disk which is $ 2 \pi \; r$ units. Thus the area of the curved side is

\[2 \pi \; r \times h \mbox{ square units.}\]

Thus the surface area of the round bar is

\[2 \pi \; r^2 + 2 \pi \; r \times h \mbox{ square units.}\]

Penny