Hi Dave,

I drew a diagram of the cone, not to scale.

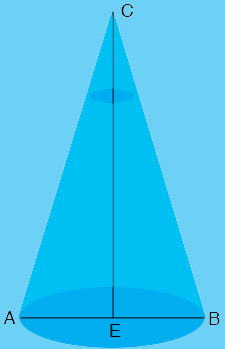
The base of the cone, at the bottom of the lake has diameter $D = |AB|$ and $E$ is the midpoint of $AB.$ The depth of the water is $d = |CE|.$ The measure of the angle $BCA$ is $20^o$ and hence the measure of the angle $BCE$ is $10^{o}.$ The tangent of the angle $BCE$ is given by

\[\tan(BCE) = \frac{|EB|}{|CE|} = \frac{D/2}{d}.\]

But $\tan(BCE) = \tan\left(10^o\right) = 0.1763$ and hence

\[D = 2 \times d \times 0.1763 = 0.353 \times d\]

Thus for your example of a depth of 10 feet the diameter of the base of the cone is approximately 3.5 feet.

Penny