Hi David,

The answer to this question is not as neat as you want. I am going to approach it graphically first taking $r = 1.$ Here is the graph of $x(t) = t - \sin(t)$ for $-16 \leq t \leq 16$ where $t$ is in radians.

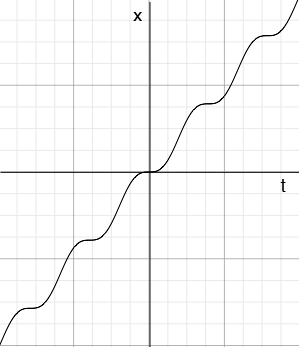
From the graph it seems that $x(t)$ is an increasing function of $t$ and a little calculus shows this is true. This is important because an increasing function has an inverse and hence the function $t(x)$ you asked for does exist. To see the graph of $t(x)$ rotate the graph above 90 degrees counterclockwise to make the $t$-axis vertical and then flip the graph around this vertical axis to orient the $x$-axis with positive to the right. The resulting graph is

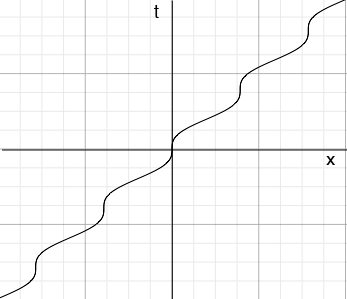
If $r$ is any positive number then $x(t) = r(t -sin(t))$ is still increasing and the inverse exists. If $r$ is negative then$x(t) = r(t -sin(t))$ is decreasing and the inverse exists.

The difficulty is to do this algebraically, that is to solve $x = r (t - \sin(t))$ for $t.$ Although $t(x)$ is a well defined function of the real number $x$ it can't be written in terms of the functions we normally use. You can't write it using polynomials, rational functions, trigonometric functions, exponential functions or logarithms.

I hope this helps,
Harley