Hi Dennie,

You didn't describe your gazebo but I expect the base is a regular polygon with an even number of sides. I am going to use $n$ for the number of sides and in my diagram of the base, $n = 8.$

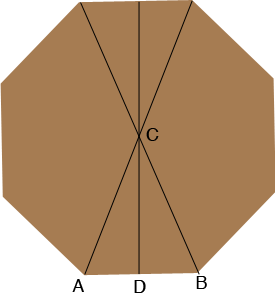
$AB$ is one of the sides and D is the midpoint of $AB.$ Since the number of sides is $n$ the measure of the angle $BCA$ is $\frac{360}{n}$ degrees and thus the measure of the angle $BCD$ is $\frac{360}{2 n}$ degrees.

Triangle $BCD$ is a right triangle and hence

\[\tan(BCD) = \frac{|DB|}{|CD|}. \]

But $|CD|$ is half of 14'6" which is 174 inches and thus half the side length is

\[|DB| = 174 \times \tan \left( \frac{360}{2 n} \right) \mbox{ inches.}\]

Penny