Hi,

I drew a diagram at a time $t$ hours. Car a is at position $A,$ car B is at position $B,$ and the intersection is at $I.$ The problem doesn't say so but I expect you are to assume that the roads intersect at a right angle.

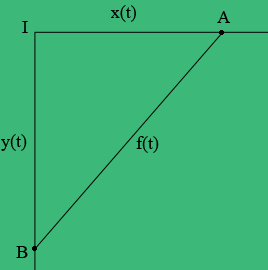
The distance from $A$ to $I$ at time $t$ hours is $x(t)$ kilometers, the distance from $B$ to $I$ at time $t$ hours is $y(t)$ kilometers and the distance from $A$ to $B$ at time $t$ hours is $f(t)$ kilometers. Use Pythagoras theorem to find a relationship between $x(t), y(t) \mbox{ and } f(t).$ Differentiate both sides of this expression with respect to $t.$

This gives you an expression involving $x(t), y(t), f(t)$ and their derivatives with respect to $t.$ At the specific time when $x(t) = 3$ km and $y(t)= 4$ km you know all the values in this expression except $f^{\;\prime}(t).$ What is this value?

Penny