Hi Jake,

Draw a unit circle with centre at the origin $O$ in the Cartesian plane.

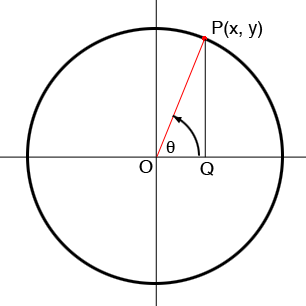
Let $P$ with coordinates $(x, y)$ be a point on the circle. Measure the angle $\theta$ between the positive $X$ axis and the ray $OP$ in radians where a positive angle is measured counterclockwise. $x$ is then the cosine of the angle $\theta$ and $y$ is the sine of $\theta,$ that is

\[x = \cos(\theta) \mbox{ and } y = \sin(\theta).\]

This is one way to define the sine and cosine and then you can define the other trig functions in terms of sine and cosine. I drew the vertical line segment $PQ$ so that you can use the triangle $OQP$ to relate the trig functions defined using the triangle to the definition I just gave using the circle. Remember that the length of $OP$ is 1.

I hope this helps,
Penny