Hi Jane,

I am not sure what measurement is 30 feet. Can you possibly sent a photo or diagram of the dome?

Penny

Jane responded

Do not have a picture
It is a Quonset under construction
Distance across base is 30 feet
Height at apex is 20 feet

Thanks Jane.

Unfortunately I can't give you an exact answer, the best I can to is approximate the length. Since the height at the apex is 20 feet I know that the curve is not half a circle. If it were a circle the height would be 15 feet so your Quonset is taller than it would be if the curve were a circle. I don't know what the curve is and I am going to guess that it is approximately a parabola.

The diagram below of a segment of a parabola is from a page on the Wolfram MathWorld site.

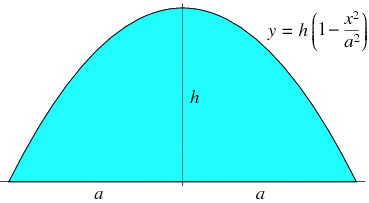
If my assumption that the curve of your Quonset is a parabola then $a = 15$ feet and $h = 20$ feet. The Wolfram MathWorld page gives the length, $s$ of the arc over the top of the Quonset as

\[s = \sqrt{a^2 + 4 h^2} + \frac{a^2}{2 h} \sinh^{-1} \left(\frac{2h}{a} \right).\]

With $a = 15$ feet and $h = 20$ feet my calculations give $s = 52.3$ feet.

I hope this helps,
Penny