Hi Jayson,

I started by drawing one section of the fire pit with $C$ at the center of the pit and D the midpoint of the line section $AB.$

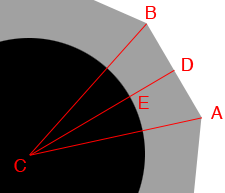
The length of $CE$ is 12.5 inches and $ED$ is 6 inches and hence the length of $CD$ is 18.5 inches. $AD$ is 6 inches and hence

\[\tan(DCA) = \frac{AD}{DC} = \frac{6}{18.5} = 0.3243\]

and thus

\[DCA = \tan^{-1}(0.3243) = 17.97 \mbox{ degrees.}\]

and hence the measure of angle $BCA$ is $2 \times 17.97 = 35.93$ degrees which is very close to one tenth of 360 degrees and thus you will need 10 bricks.

Now i can draw the entire fire pit. The triangle $BCA$ is isosceles and hence the angles $ABC$ and $CAB$ have the same measure.

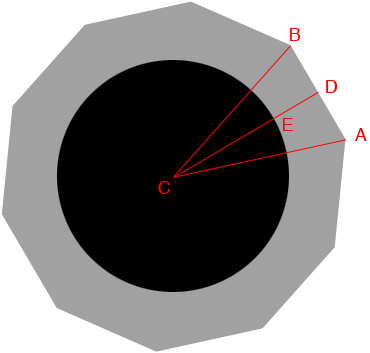
The sum of the measures of the interior angles of a triangle is 180 degrees and hence the angle measures $CAB, ABC$ and $BCA$ add to 180. Since the measure of the angle $BAC$ is 36 degrees the measure of the angle $CAB$ is

\[\frac12 (180 - 36) = 72 \mbox{ degrees.}\]

I hope this helps,
Harley