Hi Michael,

Imagine you have a large square from which you cut off each of the four corners at 45 degrees as in the diagram.

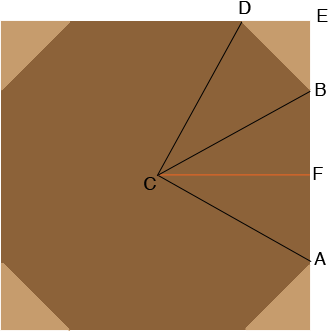
Imagine that you have done so that the short sides of the resulting octagon, $BD$ for example, measures 2 feet and the long sides, $AB$ for example, each measure 4 feet in length. Since triangle BED is a right triangle with the other two angles measuring 45 degrees each Pythagoras Theorem tells that the length of $BE$ is $\sqrt{2}$ feet. The same is true for each of the removed triangles and hence the length of each side of the square is $4 + 2\sqrt{2}$ feet. Thus if you start with a square measuring $4 + 2\sqrt{2}$ feet on each side and cut off triangles on each corner with sides of length $\sqrt{2}$ feet you will obtain the octagon you want.

If you need angle measurements then you can see that the measure of angle $FBD$ is $180 - 45 = 135$ degrees. Since the length of $CF$ is half the length of a side of the square the length of $CF$ is $2 + \sqrt{2}$ feet and the length of $FB$ is 2 feet. Hence

\[\tan(FBC)= \frac{2 + \sqrt{2}}{2}\]

and thus the measure of angle $FBC$ is

\[\tan^{-1}\left(\frac{2 + \sqrt{2}}{2}\right) = 59.64 \mbox{ degrees.}\]

Hence the measure of angle $CBD$ is $135 - 59.64 = 75.36 \mbox{ degrees.}$

I hope this helps,
Penny