| |||
| Math Central | Quandaries & Queries |
|
Question from Natalie, a student: A spherical container with radius 10cm being filled with water such that the water level, h cm, in the container increase at a rate of 0.5 cm s^(-1). Show that the area of the horizontal surface of water, A cm^(2), in the container is given by A = π(20h - h^(2) ). |
Hi Natalie,
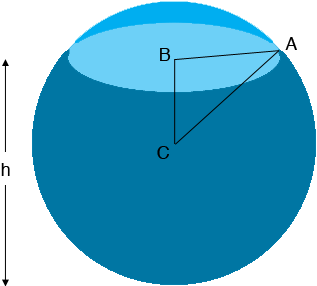
In my diagram $C$ is the centre of the sphere and $B$ is the centre of the surface of the water. Triangle $ABC$ is a right triangle and the length of $CA$ is 10 cm. What is the length of $BC?$ What does Pythagoras Theorem give you as the length of $AB?$ What is the area of the surface of the water?
In my diagram $h$ is larger than 10 cm, that is the sphere is more than half full. Does the expression for the surface area still hold when $h < 10$ cm? What if $h = 10$ cm?
Penny
 |
||
Math Central is supported by the University of Regina and the Imperial Oil Foundation.