| |||
| Math Central | Quandaries & Queries |
|
Question from Nigel: To find the area of a parallelogram you multiply the base by the height of the parallogram, the height being determined by an imaginary line drawn at right angles to the base. However if I made a parallelogram with joints at each corner and maipulated it to an upright position where the base and sides were at 90 degrees to each other,, I could then simply multiply the base times the height to get the area. Since the sloping side of the parallelogram does not vary in my imaginary jointed model, why can I not simply multiply the base by the sloping side to get the area in the same way that I multiply the base times the height of a square to find its area ? I cannot find the answer to this on the internet although I have searched. |
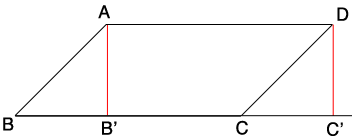
I think that if you draw an accurate picture, you will be able to see for yourself the answer to your question. I recommend drawing a parallelogram ABCD whose sides BA and CD each make a 45 degree angle with the base BC (although any angle except 90 degrees will serve as well). Now drop perpendiculars from A and D to points B’ and C’ on the base line to get a rectangle AB’C’D whose area is the same as the parallelogram you started with. (To see this, note that the right triangle ABB’ that you are discarding is congruent to the right triangle DCC’ that you are adding.) If the parallelogram’s height is 1 unit then its will equal 1*BC square units. But with a 45 degree angle at the base, the slanted side AB will have a length of sqrt(2) units, which is about 1.414 units, or 41% longer. That means that a rectangle whose base is BC and whose height equals the length of AB would have an area of about 1.414*BC, which is about 41% more than the parallelogram you started with!
Chris
 |
||
Math Central is supported by the University of Regina and the Imperial Oil Foundation.