Hi Nuraini,

Here is my diagram of the situation you describe at an arbitrary time $t$ hours.

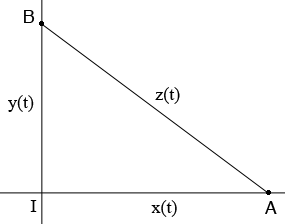
$A$ and $B$ show the position of the lorries and $I$ is the intersection. $x(t)$ is the distance from lorry $A$ to the intersection, $y(t)$ is the distance from lorry $B$ to the intersection and $z(t)$ is the distance between the lorries, all in miles. Since triangle $BIA$ is a right triangle Pythagoras Theorem gives

\[z^2(t) = x^2(t) + y^2(t).\]

Differentiate both sided with respect to $t$ and you will obtain an equation relating all three distanced and their derivatives at an arbitrary time $t$ hours.

Now focus on the time when lorry $A$ is 0.4 miles from the intersection and lorry B is 0.3 miles from the intersection. At this time you know the values of all the variables in the derivative equation except $z^\prime(t).$ Solve for $z^\prime(t).$

Penny