An isosceles triangle inscribed in a circle

HOME

Math Central

Quandaries & Queries

Question from Rachel, a student:

Triangle ABC is an isosceles triangle inscribed in circle O. If each leg of the triangle is 13cm and the altitude to the base of triangle ABC is 5cm, find the radius of the circle.

Hi Rachel,

Here is my diagram,

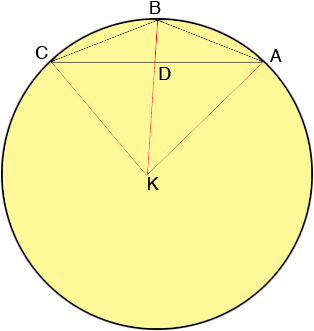
triangle and circle

$K$ is the center of the circle and $D$ is the point where the line segments $AC$ and $BK$ intersect.The first step is to show that the angle $BDA$ is a right angle and hence that $D$ is the midpoint of $CA.$ Can you see how to do this? This also ensures that angle $KDC$ is a right angle.

Let the radius of the circle be $x$ cm. Since angle $BDA$ is a right angle $BD$ is the height of the triangle $ABC$ and hence $|BD| = 5 \mbox{ cm.}$ What is the length $|DK|?$ What does Pythagoras theorem tell you about the right triangle $KDC?$ Solve for $x.$

Penny

Math Central is supported by the University of Regina and the Imperial Oil Foundation.