Hi Rahul,

Fix $\theta = 0$ and look at the $r-z$ plane identified by $\theta = 0.$ $R$ is a constant and the variable $r$ can take any value with $0 \leq r \leq R.$

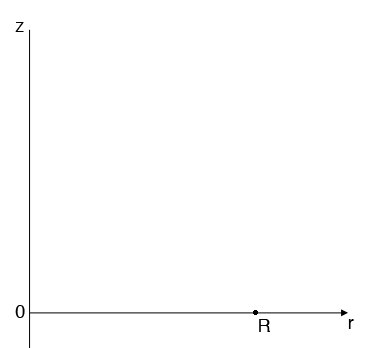
Now let $r_0$ satisfy $0 \leq r_0 \leq R.$ The points $(r_0, \theta, z)$ is to satisfy the conditions in the problem are the points $0 \leq z \leq r_0,$ that is the points on the red line segment in my diagram.

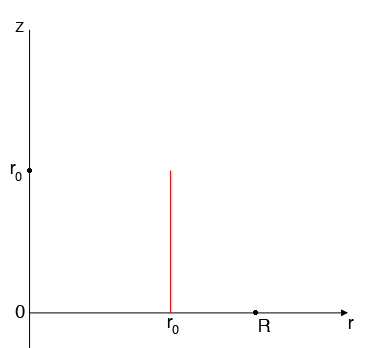
If this vertical line segment is drawn for each value of $r$ with $0 \leq r \leq R$ you get the red triangle in the diagram below.

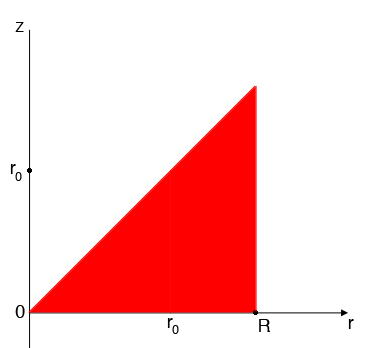
This is the region described in cylindrical coordinates by $0 \leq r \leq R, \theta=0, 0 \leq z \leq r.$ But in your question $\theta$ can take any value between $0$ and $2\;\pi.$ To construct this region you need to rotate this triangle around the z-axis to obtain a cylinder of radius $R,$ height $R$ with a conical section removed.

Penny