Rajesh,

There is not enough information to solve this problem.

I let the length of the rectangle be $L$ cm, its breadth be $B$ cm and the hypotenuse of the triangle be $H$ cm.

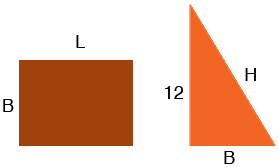
You want $2L + 2B = 12 + B + H.$ Since the triangle is a right triangle, from Pythagoras' Theorem you know that $12^2 + B^2 = H^2 .$

To illustrate that there is not enough information let $B = 5$ cm. Then using Pythagoras' Theorem $H = 13$ cm and the perimeter of the triangle is $12 + B + H = 30$ cm. Since the perimeter of the rectangle is also 30 cm you must have $L = 10$ cm.

Now suppose $B = 7$ cm then Pythagoras' Theorem gives $H = 13.89$ cm which means $L = 9.45$ cm.

Now you try one, say $B = 15$ cm. What do you get for $L?$

There are many possible values for $L.$ Is there something missing in your wording of the problem?

Penny