| |||
| Math Central | Quandaries & Queries |
|
Question from Ralph, a student: A man on a wharf 12 meters above the level of water is pulling a rope tide to a boat at the rate of 2 meters per minute. How fast is the boat approaching the wharf when there are 20 meters of the rope out. (with solution) |
Hi Ralph,
In my diagram $r(t)$ is the length of the rope at time $t$ minutes after the man started to pull the rope and $b(t)$ is the distance from the boat to the wharf at the same time. You don't know either $r(t)$ or $b(t)$ but you do know that $r^{\prime}(t) = 2$ meters per minute.
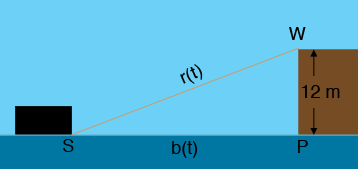
Triangle $WSP$ is a right triangle so use Pythagoras' Theorem to write an equation involving $r(t)$ and $b(t).$ Differentiate both sides with respect to $t.$
Penny
 |
||
Math Central is supported by the University of Regina and the Imperial Oil Foundation.