Hi Rose,

If you take a circular cylinder with radius $r$ cm and height $h$ cm with no top or bottom and slice tn vertically as in the diagram

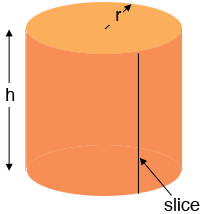
then the dark orange piece in the diagram rolls out to form a rectangle of height $h$ cm and length the circumference of the base circle which is $2 \;\pi\; r$ cm. Hence the area of this rectangle is $2 \pi r h$ square cm. The top and bottom are each disks or radius $r$ cm and hence each has area $\pi r^2$ square cm. Hence the area of the entire surface of the cylinder is

\[ 2 \pi\; r \;h + 2 \pi\; r^2 = 2 \pi \;r\; (r + h) \mbox{ square cm.}\]

Is this how you got your formula?

I think however that when the problem states the "area of the curved surface" is 880 square cm it means that the area of the dark orange region in my diagram is 880 square cm. Thus you have

\[2 \pi \;r\; h = 880 \mbox{ square cm}\]

and you know that $h = 35$ cm so

\[70 \;\pi \;r = 880 \mbox{ square cm.}\]

Solve for $r.$

Penny