Hi Samantha,

First it is important to realize that the center of the circle $x^2 + y^2 = 25$ is the origin. Here is a rough sketch of the situation.

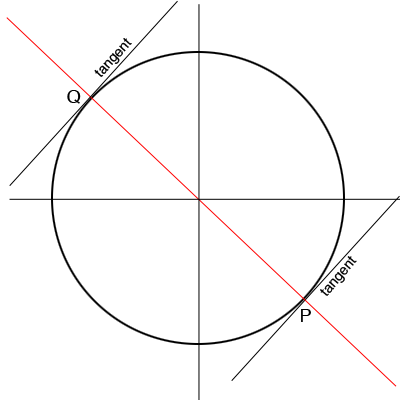
The two tangent lines are tangent to the circle at $P$ and $Q.$ By the symmetry of the circle the line joining $P$ and $Q$ passes through the center of the circle and hence is perpendicular to the two tangent lines.

What is the slope of the line joining $P$ and $Q?$ This line passes through $(0, 0).$ What is its equation? Solve this equation with the equation of the circle to find the coordinates of $P$ and $Q.$ What are the equations of the tangent lines?

Penny