Hi Shubham,

First print a copy of one centimeter graph paper. Here is a printable copy.

Step 1.

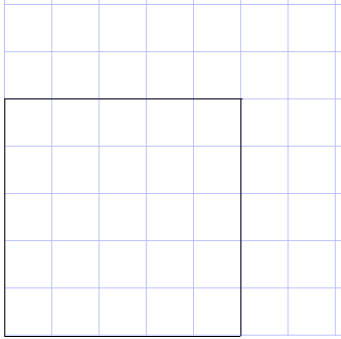
Starting at one corner of the graph paper draw a square which is 5 cm by 5 cm.

If you count the square you will see that the 5 by 5 square covers 25 of the 1 centimeter squares. Thus the area of the 5 by 5 square is 25 square centimeters.

Step 2.

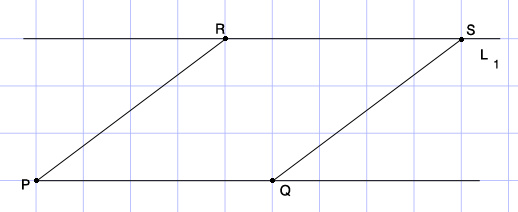
Starting at $P$ an intersection of the grid line in a different place on the graph paper draw along the horizontal grid line to a point $Q,$ 5 centimeters from $P.$ Draw the line $L_{1},$ 3 centimeters above the line segment $PQ.$ Using a ruler find the point $R$ on $L_1$ which is 5 centimeters from $P.$ Again with a ruler find the point $S$ on $L_1$ which is 5 centimeters from $R.$ If you did this carefully you will find that the line segment $QS$ has length 5 centimeters.

How many 1 centimeter squares are covered by the rhombus $PQSR?$ You can count the number of complete 1 centimeter squares covered and then match up the partial squares to obtain the number covered. This is the area of the rhombus in square centimeters.

Step 3.

Repeat step 2 with the line $L_1$ one centimeter above $PQ.$

What is the area of this rhombus?

The point I hope you see is that the area of the rhombus $PQSR$ depends on the lengths of the edges and also the shape. The smaller the angle $RPQ$ the smaller the area.

I hope this helps,
Penny