| |||
| Math Central | Quandaries & Queries |
|
Question from Timmy, a student: Joel is walking down a street and sees a 115 ft tall building in front of him. He stops 190 feet from the base of the building at the tip of the building's shadow. Round answers to three decimal places. A. If there was a piece of rope from the top of the building to Joel, how long would it be? |
Hi Timmy,
The most important step in this problem is to draw a diagram and label it. Here is my diagram.
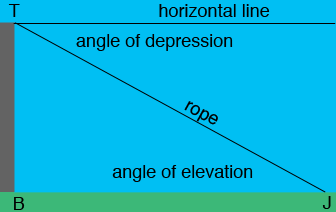
Joel is at the point $J,$ the base of the building is $B$ and the top of the building is $T.$The angle $BJT$ is the angle of elevation from Joel to the top of the building and the angle between the rope and the horizontal line is the angle of depression from the top of the building to Joel. The triangle $JTB$ is a right triangle, $|TB| = 115$ feet and $|BJ| = 190$ feet. You problem can now be solved with a little trigonometry with perhaps some help from Pythagoras.
Penny
 |
||
Math Central is supported by the University of Regina and the Imperial Oil Foundation.