Hi,

I am going to change the function slightly as I think you have copied it incorrectly. I want the expression to be

$$f(x) = \left\{ \begin{array}{ll}\frac{x^2 + 3x + 2}{x + 2} & \mbox{if $x \neq -2$}\\4 & \mbox{if $x = -2$}. \end{array} \right.$$

The value of $-2$ is important since the expression

$$\frac{x^2 + 3x + 2}{x + 2}$$

doesn't exist at $x = -2$ since the denominator is zero. Looking at the expression

$$\frac{x^2 + 3x + 2}{x + 2}$$

more closely you can see that the numerator factors so that

$$\frac{x^2 + 3x + 2}{x + 2} = \frac{(x + 2)(x + 1)}{x + 2}.$$

Thus using cancellation it seems that the expressions $\large \frac{x^2 + 3x + 2}{x + 2}$ and $x + 1$ are equal but that is not true since the first expression doesn't exist for $x = -2$ and the second expression has value $-1$ for $x = -2.$

Now back to the problem of the domain and graph of

$$f(x) = \left( \begin{array}{ll}\frac{x^2 + 3x + 2}{x + 2} & \mbox{if $x \neq -2$}\\4 & \mbox{if $x = -2$}. \end{array} \right.$$

If $x \neq -2$ then $f(x)$ is evaluated using $\large \frac{x^2 + 3x + 2}{x + 2}$ and for $x = -2, \; f(x) = f(-2) = 4$ and thus $f(x)$ exists for all real numbers $x$ and thus the domain of $f(x)$ is all real numbers.

To graph $y = f(x)$ I would start by graphing $y = x + 1$ which is the line with slope 1 and passing through $(0, 1).$

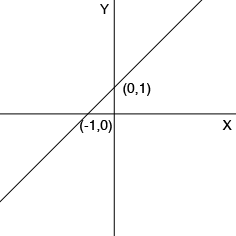
y = x + 1

We know that the functions $y = x + 1$ and $y = f(x)$ have the same values for all $x$ except $x = -2.$ At $x = -2$ we have $f(x) = f(-2) = 4$ and thus my graph of $y = f(x) is

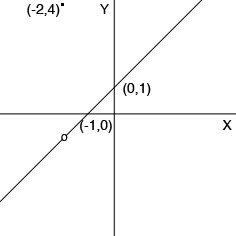
y = f(x)

The small circle on the line at $x = -2$ is to indicate that there is a "hole" in the line there and the value of $f(-2)$ is 4.

I hope this helps,
Penny