Hi Billy,

I would first sketch a graph of

\[y = \sqrt{x^2 + 2x}.\]

Here $x$ is the input variable, $y$ is the output variable.

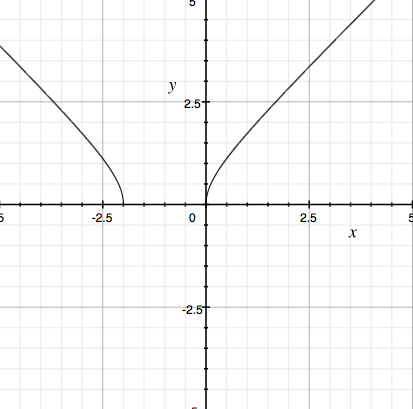
For the inverse I want to interchange the roles of $x$ and $y$ to make $y$ the input variable and $x$ the output variable. I do this on my graph by changing the labels on the axes.

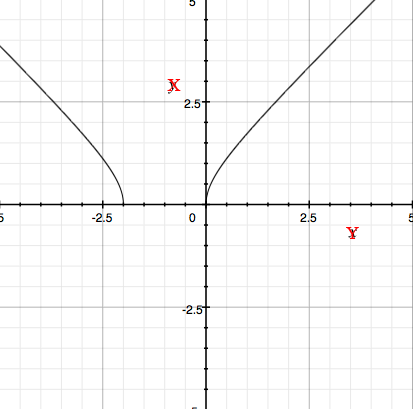
To put this graph in standard position I want the $x$ axis horizontal so I rotate the graph clockwise 90 degrees. This results in the $y$ axis vertical but with positive downwards. I then flip the graph in the horizontal axis to obtain

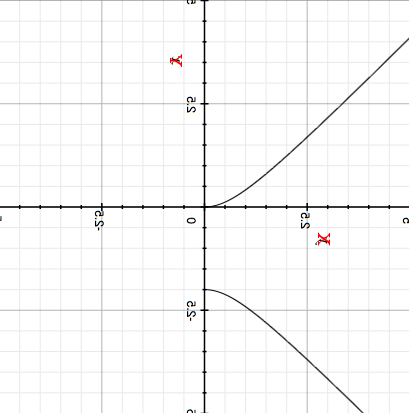
Hence the graphical analysis indicates the the inverse of

\[y = \sqrt{x^2 + 2x}\]

can be written as two functions, one that passes through $(0, 0),$ the other that passes through $(0, -2)$ and both functions have domain of $x \ge 0.$

To use an algebraic approach, with the function

\[y = \sqrt{x^2 + 2x}\]

interchange the roles of $x$ and $y$ by writing $y$ for $x$ and $x$ for $y.$ the expression then becomes

\[x = \sqrt{y^2 + 2y}.\]

Square both sides and rewrite the expression as

\[y^2 + 2y + x^2 = 0.\]

This is a quadratic in $y$ with the constant term being $x^{2}.$ Use the general quadratic to solve for $y.$ The "plus or minus" term in the general quadratic give you two expressions, one with the plus sign and the other with the minus sign. Check to see that one passes through $(0, 0),$ the other that passes through $(0, -2).$

You are not quite finished. Notice that in the original function

\[y = \sqrt{x^2 + 2x}\]

$y$ cannot be negative. This is $x$ in the inverse expressions so the domain of the inverse functions is $x \ge 0$ as was indicated by the graphical analysis.

I hope this helps,
Penny