Hi Diane,

What you call the lateral side length of a cone is often called its slant height.

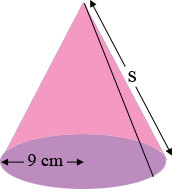
If you slice along the black line in my diagram and then roll the cone flat you obtain a sector of a circle.

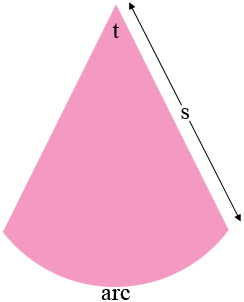
The radius of the circle that forms the arc is $s$ cm where $s$ is the lateral side length of the cone and the length of the arc is the circumference of the circular base of the cone which is $2 \pi \; r = 18 \pi$ cm. Suppose the measure of the angle that forms the circular sector is $t$ degrees.

The angle with measure $t$ degrees is a fraction of the entire angle at the center of the circle which measures $360$ degrees.

The arc with length $18 \pi$ cm is a fraction of the circumference of the circle of radius $s$ cm.

By the symmetry of the circle these fractions are the same. That is

\[\frac{t}{360} = \frac{18 \pi}{2 \pi \; s}.\]

This gives you an equation in $t$ and $s.$

You know the area of the sector is 372 sq cm and the the formula for the area of a circle gives a second equation is $t$ and $s.$

Solve these equations for $s.$

Penny