Hi

Draw a line segment 10 cm long and label the endpoints $A$ and $B.$ Set a compass to 6 cm between the point and the pencil and draw an arc above $AB$ with the center of the circle at $A.$ Without changing the distance between the point and the pencil move the point to $B$ and draw an arc above $AB$ with center $B.$ Let $P$ be the point where the arcs intersect. The triangle $ABP$ has one side of length 10 cm and two sides of length 6 cm.

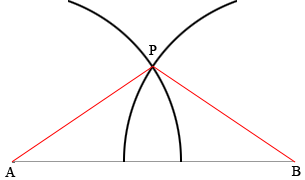
Repeat the process with the distance between the compass point and the pencil 7 cm. Repeat again with the distance 5 cm, and then again with 4 cm. Repeat again but this time with one of the arcs having radius 6 cm and the other 7 cm and then one with 6 cm and the other 3 cm.

What did you learn from your experiments?

Penny