Hi Isiah,

I am going to change your setup slightly. I want to find the equation of the circle and since the equation of a circle is easiest

\[x^2 + y^2 = r^2 \mbox{ where $r$ is the radius,}\]

when the central of the circle is at the origin I am going to move $(0, 0)$ to the centre of the circle.

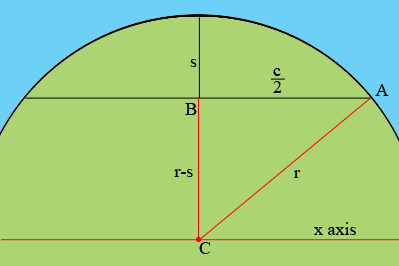
In my diagram $s$ is the length of the sagitta, $c$ is the length of the chord, $r$ is the unknown radius of the circle nd $C (0,0)$ is the centre of the circle.

Triangle ABC is a right triangle so a use of Pythagoras Theorem will allow you to solve for $r.$ Once you have the radius of the circle you can use the equation

\[y = \sqrt{r^2 - x^2}\]

to solve for $y$ for points at a distance $x$ from $C$ along the x axis. At each such point the height of the arc above the chord is $y - (r - s).$

Penny