| |||
| Math Central | Quandaries & Queries |
|
Question from Jack: I need to build a truncated cone that has a top of 30 inches and a base of 64 inches . The sides need to be at a 64.5 degree angle. This will determine the height. Can this be calculated? |
i Jack,
I drew a diagram of your truncated cone and drew a line from $B$ to intersect the base at $C.$ The length of the line segment $BC$ is $h,$ the height in inches.
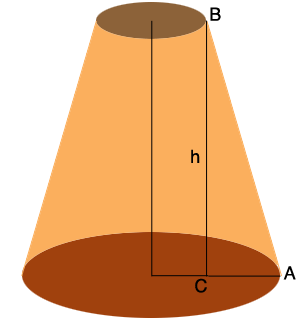
Since the radius of the top is $15$ inches and the radius of the base is $32$ inches the length of the line segment $CA$ is $32 - 15 = 17$ inches and the measure of the angle $CAB$ is $65^{o}.$ Thus
\[\tan\left(65^o\right) = \frac{h}{|CA|}\]
or
\[h = 17 \times \tan\left(65^o\right) \mbox{ inches.}\]
Penny
 |
||
Math Central is supported by the University of Regina and the Imperial Oil Foundation.