Hi Joe,

I assume this is the shape you want.

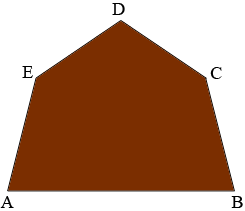
If so then the answer is yes but you don't have a lot of choice.

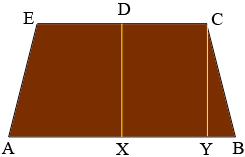
If the roof is as short as possible then $CDE$ is a straight line and the distance from $X$ to $Y$ is 4 feet.

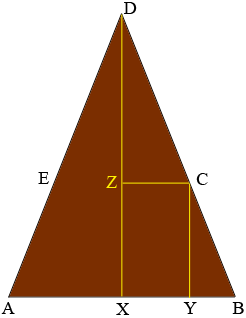
If the roof is as tall as possible then $BCD$ is a straight line and $|BC|=|CD|,$ although hey don't look equal in my diagram. Thus triangles $YBC$ and $ZCD$ are congruent and hence $|XY| = |ZC|= |YB|$ and thus the distance from $X$ to $Y$ is 3 feet.

Hence choose a point Y on the base between 3 and 4 feet from the center point $X.$ Since the triangle $YBC$ is a right triangle the height $|YC|$ can then be found using Pythagoras theorem.

\[|BC|^2 = |YB|^2 + |YC|^2\]

so

\[|YC| = \sqrt{4^2 - |YB|^2}.\]

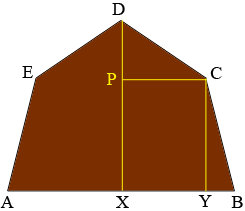
In a similar fashion

\[|PD| = \sqrt{4^2 - |PC|^2}.\]

I hope this helps,
Penny