Hi Lalitesh,

If the hexagon is regular then all the sides are of equal length and the result is obvious. I think the problem should say

"A circle is inscribed in a hexagon $ABCDEF$. Prove that $AB+CD+EF=BC+DE+FA.$"

I drew a diagram of the inscribed circle and two of the sides of the hexagon, $BC$ and $CD.$

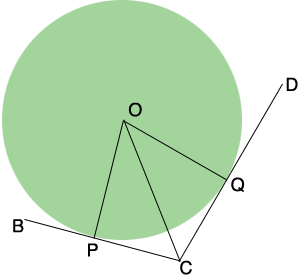
In my diagram $P$ and $Q$ are the points of tangency and $O$ is the center of the circle. Since $OQ$ is a radius of the circle and $CD$ is tangent to the circle angle $CQO$ is a right angle. Similarly angle $OPC$ is a right angle. What can you say about the length of $PC$ and $CQ?$

Penny