Hi Lauren,

I see this sequence as points on the line.

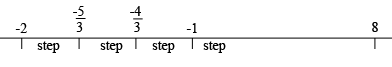
The steps are of length

\[\frac{-5}{3} - (-2) = \frac{-5}{3} + \frac{6}{3} = \frac{1}{3}\]

and

\[\frac{-4}{3} - \frac{-5}{3} = \frac{-4}{3} + \frac{5}{3} = \frac{1}{3}\]

and so on. Each step is of length $\large \frac{1}{3}.$

How many steps does it take you to get to 8?

\[-2 + \mbox{ length of a step } \times \mbox{ number of steps } = 8\]

or

\[ \frac{1}{3} \times \mbox{ number of steps } = 10.\]

Thus the number of steps is 30. At this point you need to be careful. You start at -2 and the first step gets you to the second term, the second step gets you to the third term and so on. Thus the $30^{th}$ step get yo to the $31^{st}$ term.

You can use your formula if you prefer it is just that I don't remember formulas well.

Penny