In October 2017 Reza found an error in our previous answer to this question. Below is a corrected version. Thanks for this Reza. I am always grateful that when someone finds an error in one of our pages they go to the trouble to tell us.

Harley

Hi Paul,

The Wolfram MathWorld site gives the volume $V$ of a pyramidal frustum by

\[V = \frac13 h \left( A_1 + A_2 + \sqrt{A_1 A_2} \right)\]

where $h$ is the height, $A_1$ is the bottom area and $A_2$ is the top area.

I redrew the diagram from the Wolfram site to make it more appropriate to your situation.

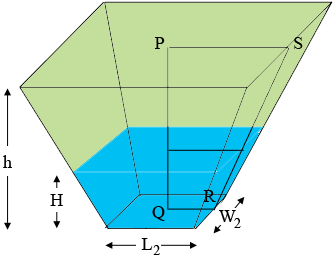
The rectangle at the base of the pond is $L_2$ units long by $W_2$ units wide, the rectangle at the top of the pond is $L_1$ units long by $W_1$ units wide, the pond is $h$ units deep and the water in the pond is $H$ units deep, $P$ is the midpoint of the top rectangle, $Q$ is the midpoint of the bottom rectangle and $R$ and $S$ are the midpoints of their respective sides. Let the rectangle formed by the surface of the water be $L_3$ units long and $W_3$ units wide.

Consider the two dimensional figure $PQRS.$

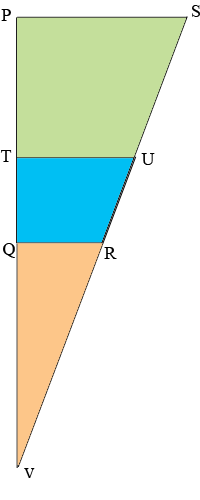
Extend the sides $PQ$ and $SR$ to meet at $V.$

\[|QR| = \frac{L_2}{2}, |TU| = \frac{L_3}{2}, |PS| = \frac{L_1}{2}, |PT| = h - H\mbox{ and } |TQ| = H.\]

Let the distance from $P$ to $V$ be $x$ feet.

The triangles $QRV, TUV$ and $PSV$ are similar and hence

\[\frac{|PS|}{|PV|}= \frac{|TU|}{|TV|} = \frac{|QR|}{|QV|}\]

and thus

\[\frac{\frac{L_1}{2}}{h+x} = \frac{\frac{L_3}{2}}{H+x}= \frac{\frac{L_2}{2}}{x}.\]

Solve

\[\frac{\frac{L_1}{2}}{h+x} = \frac{\frac{L_2}{2}}{x}\]

for $x,$ substitute into

\[\frac{\frac{L_1}{2}}{h+x} = \frac{\frac{L_3}{2}}{H+x}\]

and simplify to obtain

\[L_3 = \frac{H L_1 + (h-H)L_2}{h}.\]

In a similar fashion

\[W_3 = \frac{H W_1 + (h-H)W_2}{h}.\]

Now that you know the dimensions of the rectangle formed by surface of the water you can use the expression from the Wolfram site to calculate the volume of water in the pond.

I hope this helps,
Harley