Hi,

If possible I always start with a diagram. I used graphing software to sketch the diagram below but just a rough sketch will do. You know that $y = 2x^2 +3$ is a parabola that opens upwards and passes through $(0,3).$ The line $y = mx - 5$ passes through $(0, -5)$ and hence I can sketch a line so that it looks tangent to the parabola. There are two tangents through $(0, -5)$ but I only drew the one with positive slope. I named the point of tangency $(a, b).$

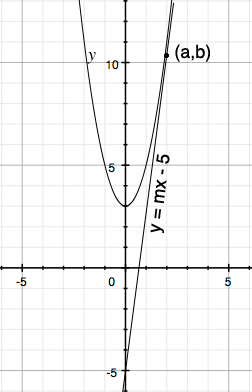
Since $(a, b)$ lies on the parabola we know that $b = 2 a^2 + 3$ and using differentiation you can find the slope of the tangent to the parabola at $(a, 2 a^2 + 3).$ Write the equation of the tangent line to the parabola at $(a, 2 a^2 + 3).$ You know that this line passes through $(0, -5).$ Solve for $a.$

Penny