A suspension bridge - Math Central

HOME

Math Central

Quandaries & Queries

Question from sai, a student:

The main cable of a suspension bridge has the shape of a parabola. The cables are strung from the top of two towers, 61 metres apart, each 15.25 metres high above the roadway. The cable is 1.5 metres above the roadway at the point that is directly between the towers.

h(x)=a(x-30.5)^2+1.5
where a is the constant and its value to be determined.

a) determine the value of the constant a by using that the fact that height of the suspension cable, h(x) is 15.25 metres at each tower. Hence, write the updated model equation.

Hi Sal,

I drew a rough diagram of the situation you described.

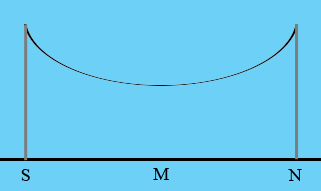
bridge

S is the tower at the south end of the bridge, N is the tower at the north end and M is the middle of the bridge. I want a coordinate system on the diagram with the surface of the bridge the X-axis with positive to the right and the Y axis vertical with positive upwards. The question is where to put the origin.

The algebraic description you have is

\[ h(x)=a(x-30.5)^2+1.5.\]

The distance from S to N is 61 metres and half of 61 is 30.5. In the algebraic expression when $x = 30.5$ you get $h(30.5) = 1.5$ metres and you know that the height of the cable is 1.5 metres at the midpoint M. Hence M is 30.5 metres from the origin and hence the origin is at S.

You know that the height of the cable above the point S is 15.25 metres but this height is $h(0).$ Solve for a.

Penny

Math Central is supported by the University of Regina and the Imperial Oil Foundation.